We will recall this tiny circuit from the past and how irritating it was to write those long equations to make the kill. Then we proceed with a particular strategy that I had not seen being employed to the problem, which kinda’ cracks it open in the first few steps.
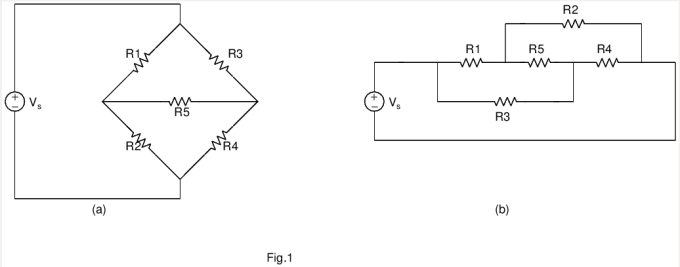
The circuit often appears in either of the two forms. We intend to analyze all the node voltages and branch currents. To make things interesting, we don’t assume any special relationship between R1, R2, R3 and R4. I hope that the reader appreciates that the problem is quite exhausting to solve using conventional methods. I will dive into my take on it right away.
In the discussion to follow, we focus on node voltages A & B and assume that any transformation on the circuit is permissible, so long as it provides the same node voltages for A &B.
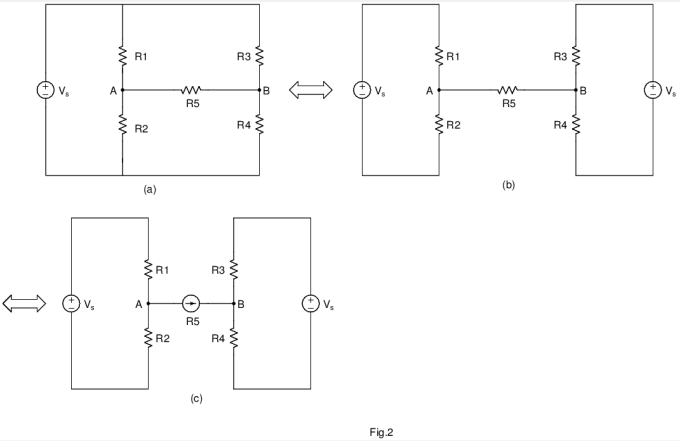
We split the voltage source in (a) into two voltage sources in (b). Now stop and think for a second, won’t this circuit just be a resistive divider, had it not been for R5? And what is it that R5 does, that ruins our day? It draws current! It loads the two nodes A & B(fig. c).
The familiar approach to best model the scenario is Thevenin’s theorem.
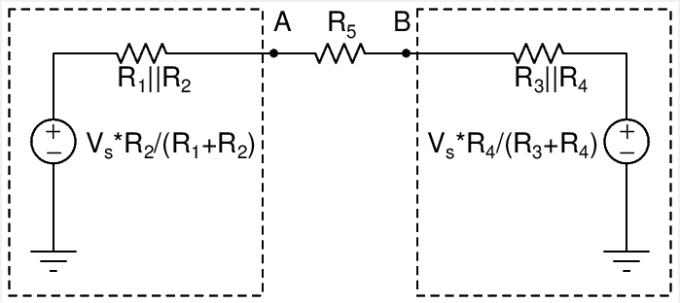
And Viola! You may now employ the good old resistive divider rules to find the node voltages A & B. Put ’em back in the original circuit and the problem cracks open.